The first-order correction to the nondegenerate state
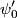 in time-independent nondegenerate perturbation theory is in time-independent nondegenerate perturbation theory is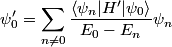 where 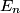 is the energy of the unperturbed state is the energy of the unperturbed state 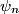 . In this case, . In this case, 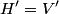 , which is an even function. , which is an even function. 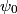 is also an even function. Therefore, whenever, is also an even function. Therefore, whenever, 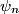 is odd, the inner product will be zero. Therefore, answer (B) is correct. is odd, the inner product will be zero. Therefore, answer (B) is correct. |